Episode 8: ML Notes (Part I): Fundamentals of Machine Learning Theory

Friday, 03/13/2020

These days I am reading the book “Machine Learning” by Tom M. Mitchell and I will be documenting some important concepts from its chapters in a series of blog posts.

[Background/Important Terminology]:

1. Machine learning is about getting good at some task T with experience E and measuring the performance by some measure P. e.g. Teaching a machine to play Ludo. The task T is to win the game. Experience E is the games played by the machine. Performance P is the proportion of games it wins.
2. Instances refer to examples in the training data.
   For example, in the following table, Outlook, Temperature, Humidity, Wind are features and Play Tennis is the output or target class. A machine is given these features and asked to predict the output class. An instance refers to a row of the table. (<Sunny, Hot, High, Weak>, No) means that for features <Sunny, Hot, High, Weak>, the target class is “No”

Source: About logic, and how to do it fast, Geniferology

1. Target Concept and Hypothesis: “Target concept” refers to the true function that maps all the features to it’s correct output. We may never find the this function because we don’t have access to all the possible examples for a concept in the world e.g. we don’t have data for all the games of Ludo ever played in time and space. But what we can do is try to guess or learn this target concept, and this learned model is then called “Hypothesis”. Hypothesis can be equal to target concept if our learning was perfect, but often hypothesis is just the best approximation of the target concept.]

Concepts:

• What is the difference between direct and indirect training examples?
  For example, in a game of Ludo, the model can be given all the different ways in which the pieces can be moved across the board (all the legal state transitions), and the set of correct moves that will result in winning/losing the game. These are direct training examples.
  Indirect training examples include all the moves made in the past and their corresponding outcome (win/loss). The model has to indirectly infer patterns from these examples. This is done by “credit assignment” which means the model has to learn the weights/credits for each move in order maximize the end reward.
  Direct training feedback is usually easier than learning from indirect feedback.

• What is Least Mean Square (LMS) training rule?
  It is a weight updating technique in which the weights are adjusted by a small amount in the direction that reduces the training error. It is used in perceptron training, stochastic gradient descent etc.

Source: Neural network for machine learning by Ujjawal

• What is concept learning?
  It means to “infer a boolean-valued function from training examples of its input and output … It can be considered as a task of searching through a large predefined space of potential hypotheses.” It’s kind of like classification.

• What is inductive learning?
  Inductive learning algorithms guarantee that the target concept will fit the training data perfectly. The core assumption in inductive learning is that the unseen data will follow the distribution of the training data so our learned hypothesis will fit the unseen data too. Formally, the inductive learning hypothesis says:
  1. Any hypothesis found to approximate the target concept well over a sufficiently large set of training examples will also approximate the target concept well over other unobserved examples.
  2. Inductive learning makes certain assumptions called inductive bias that help it classify unseen instances. For example, an inductive learner might assume that the output class can only be expressed as a conjunction (AND gate) of input variables:
     (e.g. If Temperature = High AND Wind = Weak AND Humidity = Low then class is positive).
     The leaner is biased in that it does not allow any disjunctions (e.g. Temperature = High OR Low) here.
  3. Usually inductive learners are compared based on the strength or weakness of the inductive biases they make.
     Decision Trees are an example of inductive learning, which allow disjunction of conjunctions.
     (e.g. If (Temperature = Low AND Wind = Weak) OR (Humidity = High AND Wind = Weak), Play_Tennis = Yes)).

• What is meant by syntactically and semantically distinct hypotheses?
  Consider a feature space X = [Temperature, Wind, Humidity]. Temperature can take 3 distinct values, whereas Wind and Humidity each take 2 distinct values. Then there can be 3 * 2 * 2 = 12 distinct instances with all the possible combinations of the three features.
  In this case, a hypothesis refers to a function that we try to learn in order to decide whether one should play outside or not, based on the values of X. For example:
  (<High,Weak,Low>,1) means when the temperature is high, wind is weak and humidity is low, one can play outside (Target class = 1).
  Similarly (<?,Strong,?>, 0) implies that I don’t care what the temperature or humidity is, as long as there is strong wind, I won’t play outside (target class = 0). “?” here is called a wild card.
  Moreover, (<Φ, Φ, Φ,1>) means I have no information about the features (empty instances) so I will play outside (target class = 1.
  This means that each feature can take the following values
  Temperature (3 + 2 = 5): High, Low, Medium, ?, Φ
  Wind (2 + 2 = 4): Strong, Weak, ?, Φ
  Humidity ( 2 + 2 = 4): Low, High, ?, Φ
  So, the number of syntactically distinct hypotheses is 5 * 4 * 4 = 80
  But if there is even a single Φ in the input vector, it means that values for all the other features are also unknown. In other words, if we do not know what temperature it is, we also do not know about humidity and wind. So there is a single instance where the value for all three features is null i.e. (<Φ, Φ, Φ>). So, the number of semantically distinct hypotheses is (4 * 3 * 3) + 1 = 37
  This is the entire hypotheses space that we will need to search in order to learn a concept and use machine learning to decide whether we should play outside or not.

• How do you interpret the following expressions:

1. C : X → {0,1}
   There is a target concept C that we aim to learn. X is the set of instances over which C is defined. The target concept C maps the set of instances X to a set of boolean values 0 and 1.
   Example: Predicting whether to play outside or not based a set of features X = Temperature, Wind, Humidity. In this case, C(X) = 1 means play outside. C(X) = 0 means don’t play outside.
2. (∀ x ε X)[(h2 (x) = 1) → (h1(x) = 1)] This is called more_general_than_or_equal_to rule. It means for any instance x in X, if it satisfies hypothesis h2, it also satisfies hypothesis h1, which implies that h1 is more general than h2. For example:
   H1 = <High, ? ,?> Temperature is high and I don’t care about other variables.
   H2 = <High,Weak,?> Temperature is high, wind is weak and I don’t care about humidity. H1 is more general than H2 as it will classify all instances with high wind as class = 1, where h2 is more specific and requires wind to be weak as well as temperature to be high for the output class to be 1.
3. 
   D is the training data. x is a new instance from the test set. L is a learner. The expression means that L inductively infers from the training data and test instance x that the class of x is L(x,D) = 1 (positive).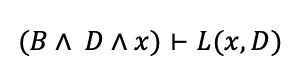
4. 
   B is the inductive bias of the learner L. This expression means that the learner “deduces” the class for test instance x, using bias B, training data D and description of test instance x.

• How is more_general_than_or_equal_to rule applied in concept learning?
  Concept learning is about finding the best hypothesis that satisfies a given training set. This partial ordering rule is useful because if we have a very large hypotheses space to search, we can order them according to their generality and test only a handful of them, thus exploiting the structure of the hypothesis space instead of exhaustively trying and testing each and every hypothesis. You start with the most specific hypothesis and generalize it each time it fails to satisfy the training set. We want to find the maximally specific hypothesis (that is general enough to perfectly fit the training data).
  The most specific hypothesis is <Φ, Φ, Φ> (you don’t classify any instance as class = 1)
  The most general hypothesis is <?,?,?> (no matter what the values of the features, you label them as class = 1)

• What is the difference between a hypothesis being consistent with a training example and a training example satisfying a hypothesis?
  H is consistent with training example x if:
  x belongs to class 1 and H also labels it as 1 i.e. (H(x) = C(x) where C is the actual target concept and H is the learned hypothesis)
  x satisfies H if:
  No matter what class x belongs to in reality, H labels it as 1 i.e. (h(x) = 1)

Topics for further exploration:

1. Version-space (set of short-listed hypotheses that satisfy the training data)
2. Candidate-elimination algorithm (it lets all the hypotheses in the version space vote for the new test instance)
3. Rote-learner algorithm (simply stores the training data in memeory and compares test data to it for classification deductively using no inductive bias.)
4. Find-S (finds the most specific hypothesis to classify later instances)

Thought of the Week:

We are in the middle of a global emergency. Couple of things you can do to survive and some updates on COVID-19:

1. Don’t go out. Even if you are able to beat the virus because you are young and fit, you might pass it on to someone else who might not be able to survive it. Be considerate.
2. Read the following books: “The Plague” by Albert Camus, “Blindness” by Jose Saramago (also a movie) (A friend’s recommendation).
3. Watch the movie Contagion.
4. Read how Singapore, Taiwan and Hong Kong are beating the pandemic [2].
5. Read about three researchers in Canada who brought the world closer to developing a vaccine for COVID-19 [3].
6. Read how Shi Zhengli, China’s “Bat Woman” is hunting down bats to trace viruses from SARS to New Coronavirus [4].
7. Wash your hands.

References:

[1] Machine Learning by Tom M. Mitchell
[2] What We Can Learn From Singapore, Taiwan and Hong Kong About Handling Coronavirus
[3] Canadian Researchers Have Isolated the Novel Coronavirus
[4] How China’s “Bat Woman” Hunted Down Viruses from SARS to the New Coronavirus

Share this: