Episode 6: What in the world is Kullback-Leibler Divergence?

Saturday, 10/26/2019

This week I discovered a new blog on topics related to Bayesian Theory and this is everything I would like to remember from a post related to Kullback-Leibler Divergence.

Concepts:

• What is Kullback-Leibler Divergence used for?
  Instead of taking the actual distribution of observed data, which may be unknown or too complex, we often approximate the distribution. KL-divergence is used to measure how much information we lose by this approximation.

• What does entropy mean in the context of information theory (or electrical engineering)?
  If we use log₂, entropy means the least number of bits we would need to encode the information. For example to encode 8, we would need (log₂(8) + 1) = 3 + 1 bits.

• What parameters do you need for creating binomial distribution?
  Number of trials (e.g. number of coin flips) = n
  Probability of each unique target value (e.g. heads and tails in a coin flip) = p

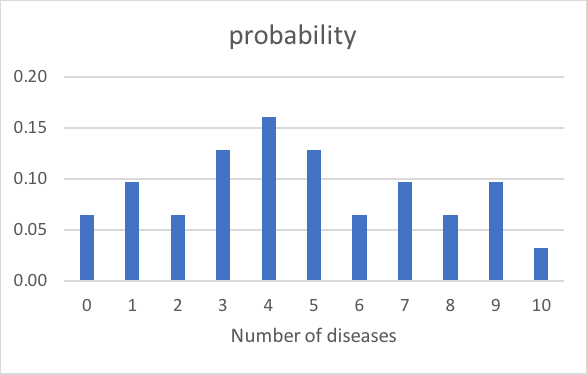
If we have a population of subjects, and they can have any number of diseases from 0 to 10, as shown in the figure above, then n = 10. We don’t know the probability p for our binomial distribution, so we calculate the mean of our observed data Using E[X] = np, we calculate p which comes out to be 4.7/10 = 0.47. So binomial distribution can be constructed using:

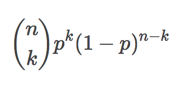
Where k goes from 0 to 10.

• Looking at the formula for KL-divergence, how can you define it in terms of expectation?

Source: Medium, A new Tool to your Toolkit, KL Divergence at Work

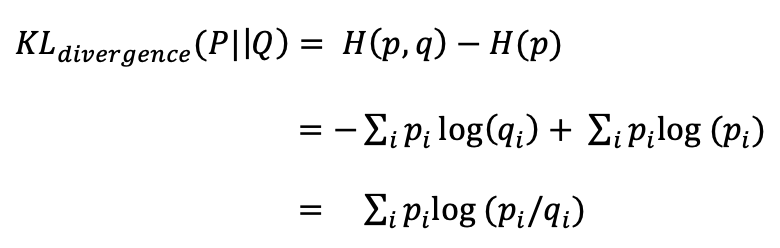
P is actual distribution and q is approximated distribution. Since expectation E[x] is defined as the product of x and its probability, K-L divergence is the expectation of the difference between log of actual distribution and log of approximated distribution.

• How is KL-divergence used as a cost function in optimization?
  We tune the parameters for our new approximated distribution by minimizing the KL-divergence. We can do this by plotting the KL-divergence value against different values of parameter p for our new distribution and choosing the value for which KL-Divergence is the least. This can also be extended to higher dimensional models with lots of parameters.

• What are some of the constraints on/properties of K-L Divergence metric? [3]?
• It is non-symmetric (“reversing the roles of the two arguments in the KL divergence can yield substantially different results”)
• It is always greater than 0. [2]
• It is only defined if P and Q both sum to 1 and Q(x) > 0 if P(x) > 0.[2]
• It has an asymptotic behavior. (because of the log terms)

• It is also known as relative entropy, or the I-divergence.

• Important applications and interesting papers on KL-Divergence?
• Model Selection, 2007 [3]
• Speech Recognition, 2004 [4]
• Speaker Identification/Image Classification, 2004 [5]

Thought of the Week:

This week I found myself in a rut when I sat down to organize my Machine Learning notes. Taking a course in Machine Learning, I have come to realize, is like going to Ikea. You like everything and you want to buy everything but you rarely need all those things at the same time. So, earlier this week, I rolled up my sleeves, picked up my data-mining shovel and decided to dig deep into the topic of bias-variance tradeoff, only to end up having a vertigo as I jumped from one concept to another, with a hundred different tabs opened up in my browser. But one good thing that came out of it was discovering a new blog on probability theory called Count Bayesie” (which is already up on my favorite list of blogs), when I was trying to find out how to expand the expectation of mean squared error (geeky segue alert!). Discovering a good resource in data science makes me realize how far I am from where I want to be in this field, but it is also like discovering a new trail along the way, a detour which might make this long, arduous journey plagued with frequent fits of self-scrutiny and imposter syndrome, more fun and exploratory. There is so much to learn and you get a day everyday to do it. What more could one ask for? Happy reading!

See you next week!

References:

[1] Kullback-Leibler Divergence Explained
[2] A new divergence measure for basic probability assignment and its applications in extremely uncertain environments
[3] The AIC Criterion and Symmetrizing the Kullback–Leibler Divergence
[4] A New Kullback–Leibler VAD for Speech Recognition in Noise
[5] A Kullback-Leibler Divergence Based Kernel for SVM Classification in Multimedia Applications

Share this: