Episode 5: Deep Learning by Ian Goodfellow, Yoshua Bengio and Aaron Courville

Wednesday, 10/09/2019

This week I read the first few chapters of the book, “Deep Learning” [1] by Ian Goodfellow, Yoshua Bengio and Aaron Courville, and this is everything I want to remember from it. (The book is available online [1] for free!)

[Background: Ian Goodfellow is famously known as the father of Generative Adversarial Networks (GANs) which he invented in 2014 for data augmentation. Earlier this year, he left Google and started working for Apple [3].

Later on, GANS became controversial as people started using them in “deepfake” face-swapping technology [3] and false news and media generation, such as the famous fake video of Donald Trump addressing the people of Belgium on climate change [2]. There is an actual website [4] called thispersondoesnotexist.com and has photos of non-existent people, generated using GANs.]

Concepts:

• What is a singular matrix?
  A singular matrix has:
  • linearly dependent columns.
  • all its eigenvalues equal to zero.
  • determinant equal to zero.
  • no inverse.

• When is it appropriate to use L1-norm?
  L2 norm increases very slowly near the origin. It is not suitable for comparing values close to zero. So when it is important to discriminate between 0 and very small non-zero values, it is desirable to use L1 norm.

• What is an orthogonal matrix?
  In an othrogonal matrix, every column is:
  • othrongonal to each other (inner product is zero)
  • every column is orthonormal (norm is 1)
    If A is an orthogonal matrix, it implies A^-1= A^T, since A^TA = AA^T

• What is an eigenvector?
  Consider a vector v with n elements. If you multiply it with a square matrix A, where A is nxn-dimensional, you will get a new nx1-dimensional vector v’.

  Now if v’ is simply a scaled version of v i.e. v’ = λ v, then v is called the eigenvector of A and λ are eigenvalues of A. Even if you use some scaled version of v, say sv where s ≠ 0, eigenvalues of A remain the same.

• When is a matrix positive semi-definite?
  Matrix with positive eigenvalues is positive definite.
  Matrix with positive or zero eigenvalues is positive semidefinite. ∀ x , x^TAx ≥ 0

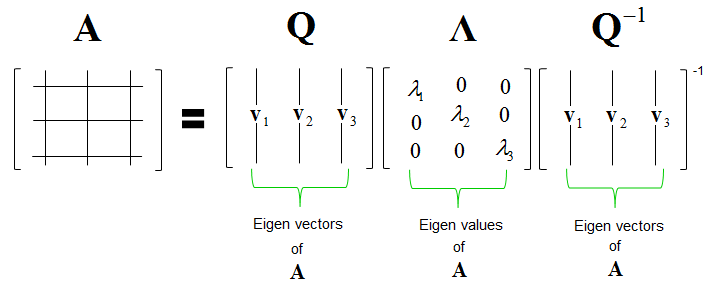
• What is eigenvalue decomposition?
  A = VDV^-1
  Where:
  V = concatenate all eigenvectors of A in one matrix V. It will be an orthogonal matrix.
  D = Put all eigenvalues of A in a diagonal matrix D

  A needs to be positive semidefinite in order to be able to decomposed this way.

Source: Share Tech Note

• What is singular value decomposition?
  Unlike eigenvalue decomposition, every matrix has SVD.
  A = UDV^T
  Where:
  U = Contains left singular vectors of A. These are equal to the eigenvectors of AA^T [5]
  V = Contains right singular vectors of A. These are equal to the eigenvectors of A^TA [5]
  D = Diagonal matrix that contains singular values of A. These are equal to the square roots of eigenvalues from AA^T or A^TA. [5]

Source: Blogs.Oracle

• What is the difference between Probability Theory and Information Theory?
  Probability theory allows us to make uncertain statements and to reason in the presence of uncertainty.
  Information theory enables us to quantify the amount of uncertainty in a probability distribution.

• What is the difference between Frequentist and Bayesian Probability?
  The kind of probability related to the rates at which events occur (drawing cards, tossing coins) is called frequentist probability.
  The one that is related to qualitative levels of certainty (disease diagnosis) is known as Bayesian probability.

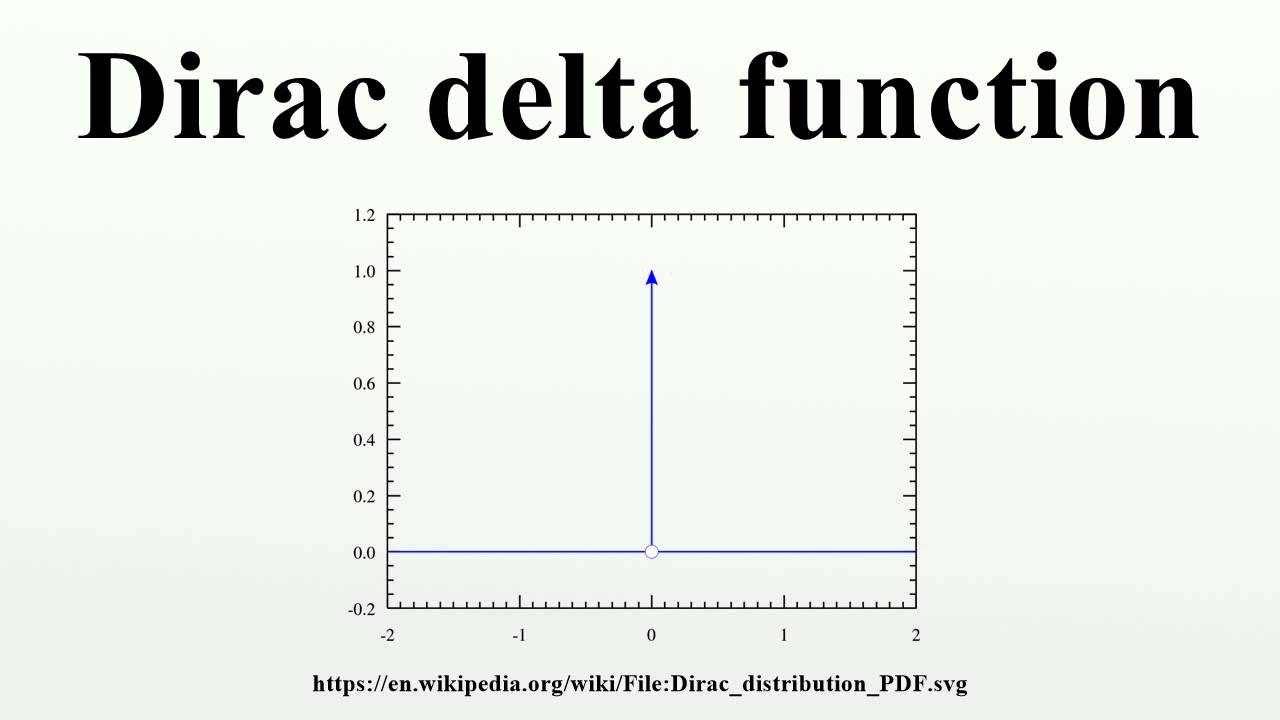
• What is so special about the delta function?
  Dirac delta function is defined such that it is zero valued everywhere except 0, yet integrates to 1. It is a special kind of function called generalized function that is defined in terms of its properties when integrated.

Source: WikiAudio

Thought of the Week:

I found this really useful image shared by Dr. Zeeshan-ul-hassan Usmani on his LinkedIn [6], a couple of weeks ago. He is originally from Pakistan and currently works as a Data Science, AI & Blockchain expert in Claifornia. I think the following image is helpful in learning how to go about machine learning in a sensible and systematic way, instead of going down the rabbit hole, randomly hunting for classifiers and never coming back!

See you next week!

References:

[1] Deep Learning
[2] You thought fake news was bad? Deep fakes are where truth goes to die
[3] Father of GANs Ian Goodfellow Splits Google For Apple
[4] Fake image website
[5] Singular Value Decomposition (SVD) tutorial
[6] Dr. Zeeshan-ul-hassan Usmani, LinkedIn

Share this: